



Next: Overview
Up:
Previous: Volume:
Contents
Subsections
- Overview
- About random numbers
- Generation of Random Numbers
- Congruential Generators
- which defines
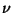 as being congruent
to n modulo m. It means that
as being congruent
to n modulo m. It means that
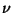 is the remainder
is the remainder
- Provided an initial seed
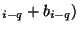 is supplied,
a string of distinct values can be generated.
is supplied,
a string of distinct values can be generated.
- By taking
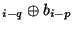 we find a sequence
of numbers distributed on [0,1].
we find a sequence
of numbers distributed on [0,1].
- In the linear congruential generator, only one previous random variable
is used to derive the next one, we can use more of the earlier generated numbers,
each associated with a specified multiplier - a compound generator. If the last
k generated numbers are used, we can write
- where
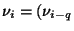 and the set of multipliers is a= (a
and the set of multipliers is a= (a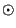 a
a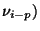 ,..,a
,..,a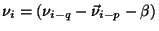 ).
By taking a value of just 2 for k and suitable multipliers a
).
By taking a value of just 2 for k and suitable multipliers a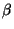 and
a
and
a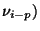 , a compound generator with acceptable result structure
can be obtained, described next.
, a compound generator with acceptable result structure
can be obtained, described next.
- Shift-Register Generators
- Fibonacci generators
- We can generate a sequence of numbers, given that the first p numbers
are provided e.g. from a multiplicative congruential generator. The operation
denoted by
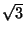 is conventionally the `exclusive-or'.
It may be however just simple addition or subtraction, and recent studies favour
the latter operation, giving rise to a subtracted Fibonacci generator.And especially
interesting development is the subtract-with-borrow generator of this type.
The algorithm is
is conventionally the `exclusive-or'.
It may be however just simple addition or subtraction, and recent studies favour
the latter operation, giving rise to a subtracted Fibonacci generator.And especially
interesting development is the subtract-with-borrow generator of this type.
The algorithm is
- The `carry' coefficient,
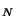 , which must
be set to 0 or 1, arbitrarily, at initialization, is reassigned in each call
as follows; if the quantity in brackets is negative, so that m must be added
to it to carry out the modulo m operation,
, which must
be set to 0 or 1, arbitrarily, at initialization, is reassigned in each call
as follows; if the quantity in brackets is negative, so that m must be added
to it to carry out the modulo m operation,
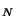 is
set to zero otherwise it assumes the value unity. If m, p, and q satisfy certain
conditions, the period of this generator is m
is
set to zero otherwise it assumes the value unity. If m, p, and q satisfy certain
conditions, the period of this generator is m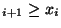 -m
-m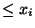 .
.
- Practical generators-Super Duper
- Unra generator in CECILE
- Testing random Number Sequences
Amaury LATAILLADE
2002-11-04
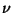 as being congruent
to n modulo m. It means that
as being congruent
to n modulo m. It means that
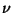 is the remainder
is the remainder
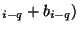 is supplied,
a string of distinct values can be generated.
is supplied,
a string of distinct values can be generated.
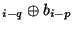 we find a sequence
of numbers distributed on [0,1].
we find a sequence
of numbers distributed on [0,1].
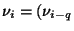 and the set of multipliers is a= (a
and the set of multipliers is a= (a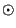 a
a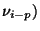 ,..,a
,..,a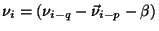 ).
By taking a value of just 2 for k and suitable multipliers a
).
By taking a value of just 2 for k and suitable multipliers a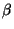 and
a
and
a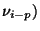 , a compound generator with acceptable result structure
can be obtained, described next.
, a compound generator with acceptable result structure
can be obtained, described next.
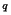 , and the first p bits are provided; the constant
c has been set equal to zero. There is a maximum of
2
, and the first p bits are provided; the constant
c has been set equal to zero. There is a maximum of
2
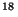 distinct possible iterations before sequence repeats
itself.Interesting is the existence of sequences with only two non-zero coefficients,
i.e. b
distinct possible iterations before sequence repeats
itself.Interesting is the existence of sequences with only two non-zero coefficients,
i.e. b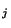 is of the form
is of the form
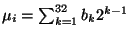 denotes
the `exclusive or' operation.
denotes
the `exclusive or' operation.
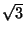 is conventionally the `exclusive-or'.
It may be however just simple addition or subtraction, and recent studies favour
the latter operation, giving rise to a subtracted Fibonacci generator.And especially
interesting development is the subtract-with-borrow generator of this type.
The algorithm is
is conventionally the `exclusive-or'.
It may be however just simple addition or subtraction, and recent studies favour
the latter operation, giving rise to a subtracted Fibonacci generator.And especially
interesting development is the subtract-with-borrow generator of this type.
The algorithm is
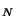 , which must
be set to 0 or 1, arbitrarily, at initialization, is reassigned in each call
as follows; if the quantity in brackets is negative, so that m must be added
to it to carry out the modulo m operation,
, which must
be set to 0 or 1, arbitrarily, at initialization, is reassigned in each call
as follows; if the quantity in brackets is negative, so that m must be added
to it to carry out the modulo m operation,
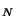 is
set to zero otherwise it assumes the value unity. If m, p, and q satisfy certain
conditions, the period of this generator is m
is
set to zero otherwise it assumes the value unity. If m, p, and q satisfy certain
conditions, the period of this generator is m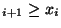 -m
-m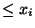 .
.
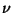 degrees of freedom as
degrees of freedom as