Next: Correlations in random number
Up: Correlations in random numbers
Previous: Correlations in random numbers
Contents
Super duper : normal and cumulative distributions
We formed also the corresponding cumulative distributions and apply Kolmogorov-Smirnov
test.
Kolmogorov-Smirnov statistics:
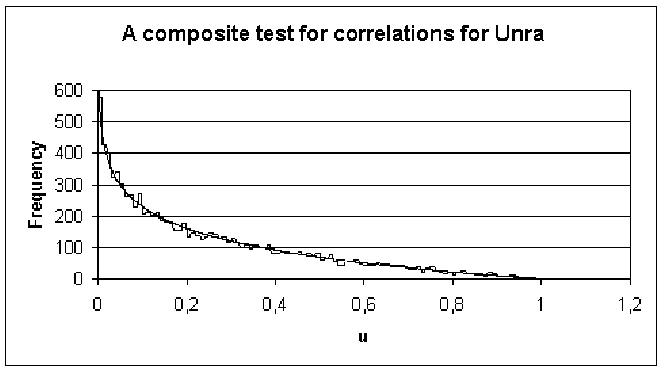
- unra: q=0.814 -> f=25.16%
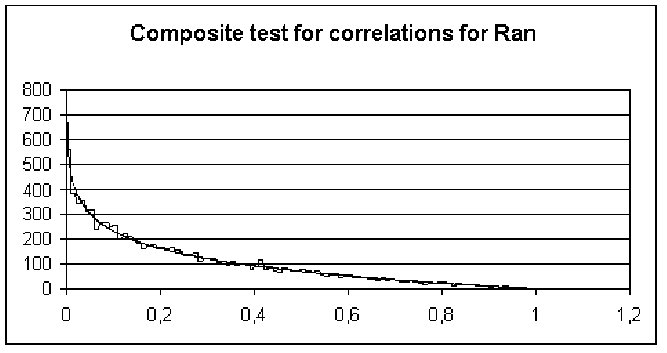
- ran: q=1.227 -> f=3.50 %
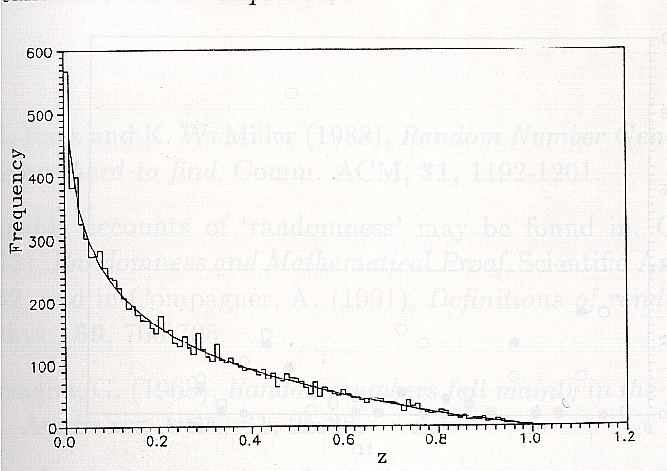
- super duper: q=0.957 f=15.3 %
The f is probability of getting a value larger than q in a sample of size 200
in comparison of cumulative distributions.




Next: Correlations in random number
Up: Correlations in random numbers
Previous: Correlations in random numbers
Contents
Amaury LATAILLADE
2002-11-04