 ), i=1,...,N-1 were
histogrammed into k
), i=1,...,N-1 were
histogrammed into k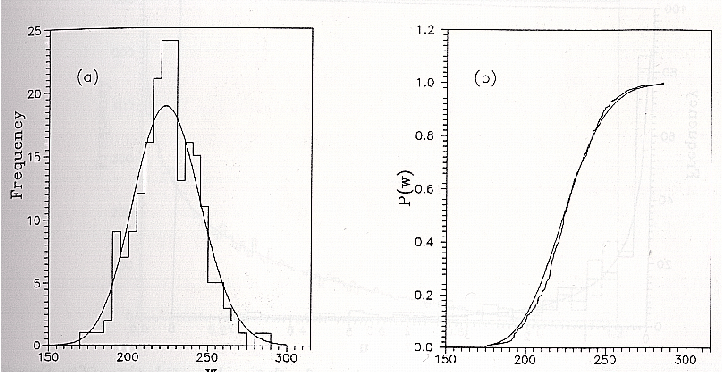 sub squares with k=16, so for each from 16
sub squares with k=16, so for each from 16 subsquares
we have number n
subsquares
we have number n ,i=1..16,j=1..16, which equals number of occurencies
of pairs in those square. the following quantities were formed,
,i=1..16,j=1..16, which equals number of occurencies
of pairs in those square. the following quantities were formed,
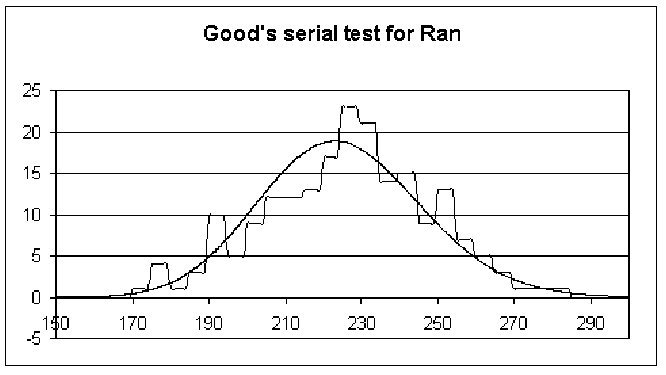
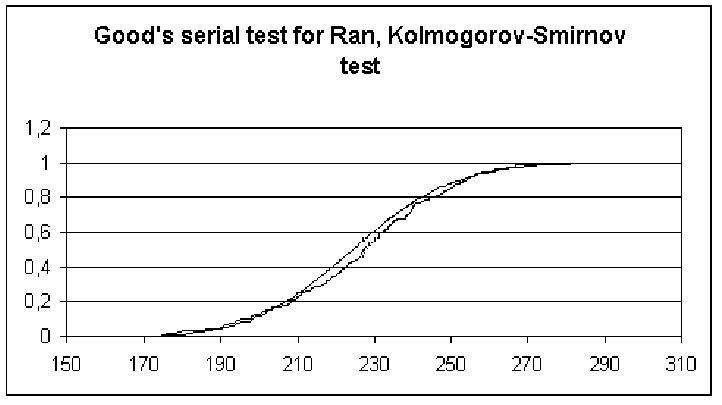
For each of 200 samples, each sample has 10000 variates, we take an overlapping
pairs of numbers. The N-1 points (
 ), i=1,...,N-1 were
histogrammed into k
), i=1,...,N-1 were
histogrammed into k sub squares with k=16, so for each from 16
sub squares with k=16, so for each from 16 subsquares
we have number n
subsquares
we have number n ,i=1..16,j=1..16, which equals number of occurencies
of pairs in those square. the following quantities were formed,
,i=1..16,j=1..16, which equals number of occurencies
of pairs in those square. the following quantities were formed,
 e
e
and
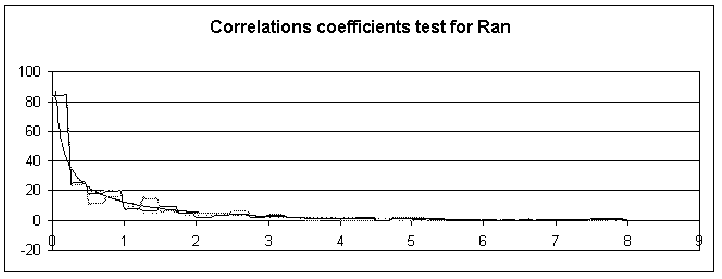
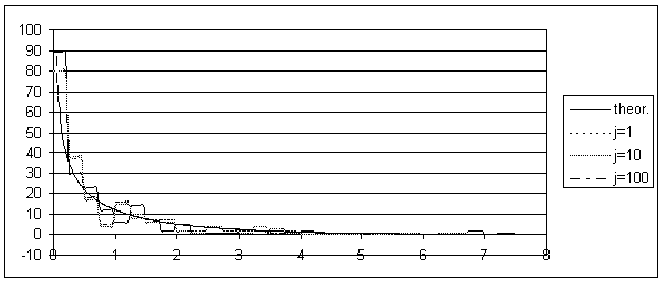
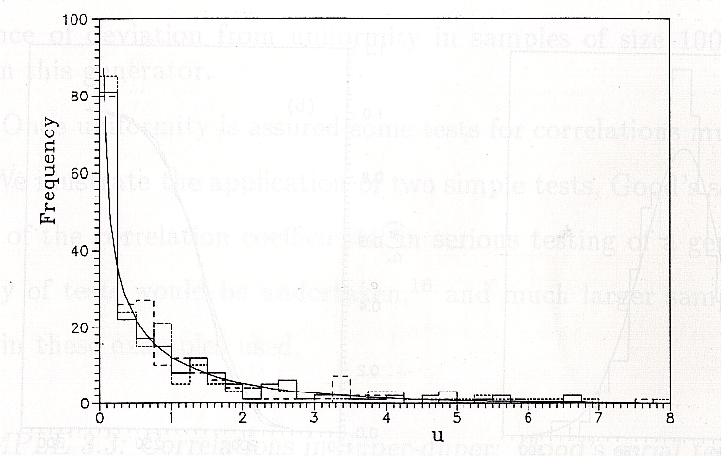
The statistic w is defined by
 t
t