where , it should follow the distribution with =150 degrees of freedom.

Next: Correlations in random numbers Up: Testing of uniformity. Previous: Testing of uniformity. Contents

where $\overline{n}=N/k\protect$ , it should follow the $\chi ^{2}\protect$ distribution with $\nu \protect$ =150 degrees of freedom.

This was done for 200 samples, the histogram of these values is compared with p 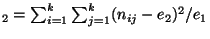$_{\chi ^{2},\nu }(T)$ in following pictures.

$\resizebox*{1.2\columnwidth}{!}{\includegraphics{pic/unraunif.ps}}$

$\resizebox*{1.1\columnwidth}{!}{\includegraphics{pic/ranunif.ps}}$

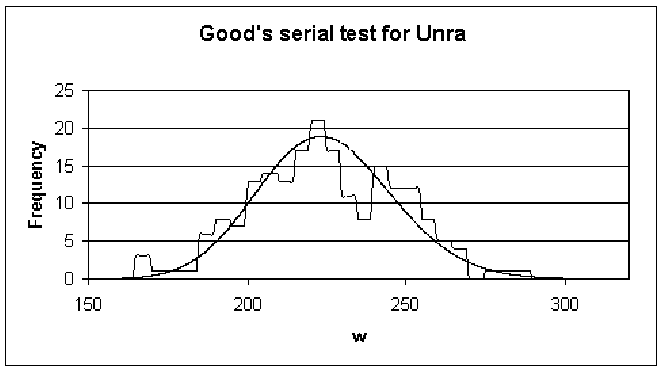
Uniformity of Super-duper:

$\resizebox*{1.1\columnwidth}{!}{\includegraphics{pic/supunif.ps}}$

The cumulative frequency from the histogram was compared with P 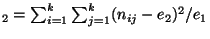$_{\chi ^{2},\nu }(T)$ and the Kolmogorov-Smirnov Statistic q, defined earlier, formed.

Unra q=0.486 -> f= 60.1 %.
Ran q=0.5144 -> f=56.73 %
Super Duper q=0.606, f=46 %

where f% means probility of obtaining larger value than q in such a comparision with the predicted 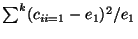$\chi ^{2}\protect$ distribution. Since this is the test of uniformity, we can conclude there is no significant evidence of deviation from uniformity in samples of size 10000 drawn from Super Duper and Ran generator. Unra, however has larger deviation and it can be considered not as uniform as other two generators.

Next: Correlations in random numbers Up: Testing of uniformity. Previous: Testing of uniformity. Contents

Amaury LATAILLADE 2002-11-04