next up previous contents
Next: A composite test for Up: Testing random Number Sequences Previous: The distribution of this   Contents

Correlations in random number generators: Correlation coeficients

In this test we choose the j separation correlations test for samples of 10000 variations. We take the sample of 10000 random numbers and the estimation of the correlation coeeficients are

r\( _{j} \)= 12(< \( \xi _{i}\xi _{i+j}>-1/4)=12(<(\xi _{i}-1/2)(\xi _{i+j}-1/2)>) \)

for j=1,10 and 100

The relevant statistics is u=Nr\( _{j}^{2} \) which, independent of j, can be shown to approximately have the chi-square distribution with one degree of freedom. For each of the three values of j, 200 such coefficients were determined.Their distribution is shown in following figures.

Unra:



\resizebox*{1.2\columnwidth}{!}{\includegraphics{pic/unraccoef.ps}}





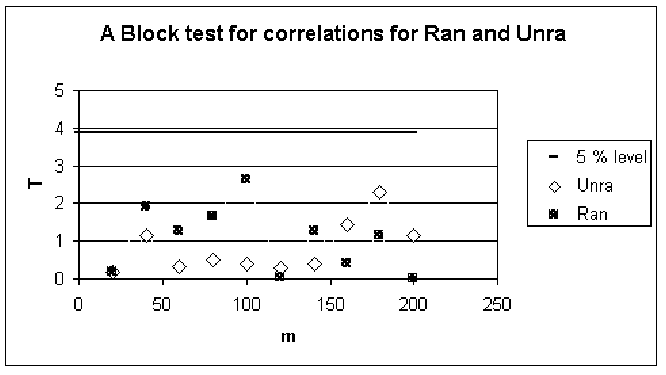
\resizebox*{1.3\columnwidth}{!}{\includegraphics{pic/ranccoef.ps}}



Super-duper:



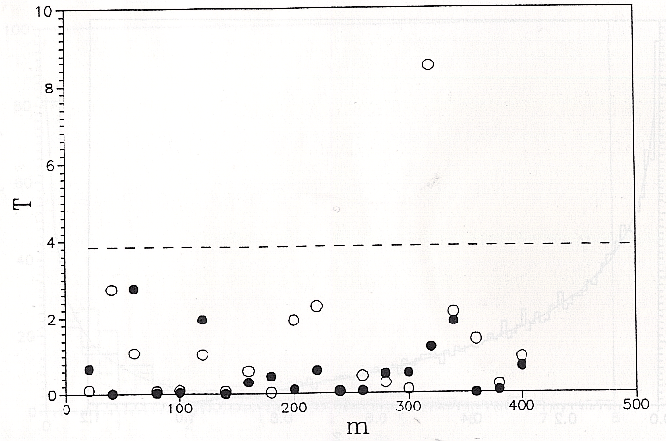
\resizebox*{1.3\columnwidth}{!}{\includegraphics{pic/supccoef.ps}}



We can see there is no evident deviance from theoretical distribution in any of renadom numbers generators


Amaury LATAILLADE 2002-11-04