 y mas tarde en castellano
y mas tarde en castellano  .
.
Avertissement
Cette page est conçue pour résumer la cavitation acoustique en quelques articles, à l'usage de personne débutant dans le domaine, ou ayant peu de temps à y investir. Sa motivation essentielle est le partage d'une expérience et d'une bibliographie. En temps que résumé, elle est forcément incomplète. En tant que page WEB non soumise au filtre du ``peer-reviewing'', elle est susceptible de contenir des erreurs et des points de vue personnels de l'auteur. Si vous estimez que tel est le cas, vous pouvez m'en faire part par Email. Cette page est libre et peut être à ce titre référencée sur un autre site. Si vous le faites, merci de m'en faire part. Si cette page vous a été utile, un petit mail m'encouragera à la faire progresser.
This page will be soon traduced in English  y mas tarde en castellano
y mas tarde en castellano  .
.
La coalescence intervient du fait du mouvement relatif de deux bulles sous l'influence des force de Bjerknes primaire et secondaire. La primaire provoque un mouvement relatif à elle seule, mais la secondaire fournit de plus une interaction attractive dans certains cas.
L'évolution d'une population de bulles liée à la coalescence a été traitée théoriquement (3,1,2,4). On considère généralement qu'il y a coalescence dès qu'il y a contact, sans tenir compte d'un éventuel choc élastique ou d'un temps de drainage du liquide à l'interface. Le problème est traité en calculant un noyau de probabilité de collision à partir d'une section de collision.
Naturellement, dans un liquide juste à saturation, c'est-à-dire à l'équilibre avec une atmosphère à 1 bar, une bulle de gaz a tendance à se dissoudre, car la pression dans la bulle est supérieure à la pression dans le liquide, à cause de la tension superficielle. La concentration en gaz dissous au voisinage de la bulle est donc supérieure à celle infiniment loin de celle-ci ce qui cause un flux de gaz centrifuge, qui "dégonfle" la bulle.
Lorsque la bulle oscille, la pression dans la bulle varie autour de la pression d'équilibre, et il en est de meme du flux de gaz: pendant la phase d'expansion, la bulle se remplit de gaz, pendant la phase de compression, elle se vide.
Ce qui est intéressant c'est le flux de gaz moyen sur une période. Comme la surface d'échange est plus grande pendant l'expansion, on peut concevoir qu'en moyenne il rentre un peu plus de gaz qu'il n'en sort, ce qui conduirait à faire gonfler lentement la bulle. Ce comportement entre donc en compétition avec la tension superficielle, et pour une pression acoustique suffisante, la bulle a tendance à croître en moyenne, ou plus précisément à augmenter sa masse de gaz et donc son rayon ambiant. Ce seuil de pression acoustique s'appelle seuil de diffusion rectifiée: juste en ce point, la bulle ni ne grossit, ni ne se dissout (5,6).
La théorie linéaire prédit que ce point d'équilibre est instable: si la bulle grossit juste un peu, alors elle continue à grossir indéfiniment, ce qui signifie pratiquement qu'une bulle ne peut osciller indéfiniment en conservant toujours la même masse de gaz. (7)
Cela est en contradiction avec l'observation de la sonoluminescence à une bulle (SBSL) expérience au cours de laquelle la bulle peut conserver le même rayon ambiant pendant plusieurs jours. Cet effet est une conséquence de la non-linéarité des oscillations et a fait l'objet de nombreuses publications depuis les années 1990 (9,8).
Une théorie très complète et fournissant le taux de croissance d'une bulle meme loin du seuil a été développée par (10).
La force de Bjerknes est une force d'Archimède généralisée. De manière générale (primaire ou secondaire) c'est la force que subirait le volume de fluide qui remplacerait la particule. Elle résulte des différences de pression appliquées aux bornes de ce volume de fluide:
où ![]() est la pression qui s'exercerait sur la surface matérialisant
la frontière de la particule si cette particule était remplacée par
du fluide.
est la pression qui s'exercerait sur la surface matérialisant
la frontière de la particule si cette particule était remplacée par
du fluide.
Dans le cas d'un champ acoustique, une première contribution à ce
terme de pression est la pression engendrée par l'onde ou pression
acoustique. Si la longueur d'onde est très grande devant la
particule, le gradient de pression peut etre considéré comme
homogène dans tout le volume ![]() (on néglige les termes correctifs
d'ordre 2), et l'expression devient simplement:
(on néglige les termes correctifs
d'ordre 2), et l'expression devient simplement:
où ![]() est le gradient de pression estimé au centre de la
bulle si elle était absente.
est le gradient de pression estimé au centre de la
bulle si elle était absente.
Il apparaît que pour une bulle dans un champ acoustique, cette force est le produit de deux termes oscillants: le volume de la bulle et le gradient de pression. La moyenne sur une période de cette force est donc en général non nulle, et liée au déphasage de ces deux grandeurs. Dans l'approximation linéaire, on montre que la force moyenne subie par une bulle est dirigée vers les ventres de pression pour une bulle de taille inférieure au rayon de résonance, et vers les noeuds pour une bulle de taille supérieure au rayon de résonance.
Cette conclusion doit être nuancée dans un cadre non-linéaire en vertu des nombreuses résonances non-linéaires.
Il importe enfin de bien comprendre que cette force n'est pas la seule qui s'exerce sur la bulle : cette dernière subit également des forces liées au mouvement relatif des deux phases (masse ajoutée, trainée visqueuse, force d'histoire). La force de Bjerknes n'inclut que la force qui s'exercerait sur une sphère liquide équivalente soumise aux même champ d'accélération, et est bien en cela une force d'Archimède généralisée.
L'origine est la même que pour la force de Bjerknes primaire. Mais on prend en compte, en plus du champ d'accélération produit par l'onde acoustique, le champ d'accélération produit par une bulle voisine. Le produit de celui-ci par les variations de volume étant ici encore à moyenne non nulle, il résulte une force nette non nulle en moyenne sur une période, dirigée selon l'axe liant les centres des deux bulles.
La théorie linéaire prédit alors, une attraction entre des bulles de rayons ambiants situés du même coté du rayon de résonance, et une répulsion dans le cas contraire. Ici encore en raison des résonance non-linéaires, cette conclusion est fausse pour des champs acoustiques importants : il a été montré notamment par la théorie que deux bulles de taille légèrement différentes, mais toutes deux bien plus petites que le rayon de résonance (disons de l'ordre de quelques microns) pouvaient se repousser dans un champ acoustique de 20 kHz, ce qui expliquerait partiellement les filaments de bulles visibles dans toute expérience de cavitation forte.
C'est l'aspect le moins connu de la cavitation en raison de la l'intervalle de temps sur lequel il se produit. Cependant, de nombreuses théories traitant des instabilités de surface de la bulle existent (11,12), et ont été utilisées (9,13,14,15) pour expliquer la disparition d'une bulle unique dans une expérience de SBSL au-delà d'une excitation critique (16,17,18). Ces théories se basent sur une étude de stabilité linéaire.
Un seuil d'apparition de ces instabilités peut donc étre déterminé dans l'espace des paramètres. Dans certains cas ces instabilités peut conduire à la fragmentation, dans d'autres non. Pour conclure sur la fragmentation ou non, une étude non-linéaire est nécessaire (19).
On peut mentionner un ordre de grandeur intéressant: a une fréquence
de l'ordre de 20 kHz, pour des pressions acoustiques variant entre 1
et 1.5 bars, le seuil d'instabilité (théorique et déterminé
expérimentalement) est de l'ordre de quelques microns, ce qui
signifie que l'existence de bulles plus grosses ne peut être que
fortuit. Ceci discrimine l'argument souvent avancé, selon lequel les
bulles produisant des effets sonochimiques seraient des bulles
résonantes. En effet le rayon de résonance à cette fréquence est de l'ordre de
160 ![]() m, ce qui est bien supérieur au seuil sus-mentionné.
m, ce qui est bien supérieur au seuil sus-mentionné.
En fait pour produire des effets, une bulle doit simplement imploser
(on parle de bulle inertielle), ce qui est le cas au-dessus du
seuil de Blake (de l'ordre de 1
![]() m pour une pression acoustique de 1.5 atm), donc pour des
bulles très petites.
m pour une pression acoustique de 1.5 atm), donc pour des
bulles très petites.
Une bulle de gaz dans un liquide au repos peut osciller radialement (mais pas seulement) autour de son rayon ambiant. Il suffit de s'imaginer que l'on écarte légèrement la bulle de ce rayon ambiant et qu'on la relache. L'élasticité du gaz tend à ramener la bulle vers son rayon ambiant, mais ce faisant, le liquide est mis en mouvement radial. Or ce dernier possède une certaine inertie, et le système va donc osciller autour de son point d'équilibre. La bulle peut être vue comme un oscillateur mécanique masse (le liquide)-ressort (la bulle). Dans l'absolu ces oscillations sont non-linéaire et son données par une équation différentielle non-linéaire, par exemple l'équation de Rayleigh. Si l'on traite de petites oscillations, cette équation peut être linéarisée, et on montre que la fréquence de résonance angulaire de l'oscillateur harmonique obtenu s'écrit:
![$\displaystyle \omega_0 =\left\{\frac{p_0}{\rho R_0^2} \left[3\eta\left(1+W \right)-W \right] \right\}^{1/2}$](lexique-img7.png) |
où
![]() est la tension de Laplace adimensionnelle,
et
est la tension de Laplace adimensionnelle,
et ![]() l'exposant polytropique (compris entre 1 et
l'exposant polytropique (compris entre 1 et ![]() ).
Pour des bulles supérieures à quelques
).
Pour des bulles supérieures à quelques ![]() m dans des conditions
standards,
m dans des conditions
standards, ![]() , et on obtient plus simplement:
, et on obtient plus simplement:
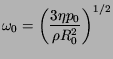 |
Les principales causes de dissipation amortissant ce mouvement radial propre sont les gradients thermiques dans le gaz (surtout à basse fréquence), la viscosité du liquide, et la compressibilité du liquide (surtout à haute fréquence) (20).
Notations classiques : ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Amplitude de l'oscillation de pression engendrée localement par l'onde acoustique. Pour les modèles de bulle unique, cette grandeur peut être vue comme l'amplitude d'oscillation de pression infiniment loin de la bulle, ou comme celle qui existerait au centre de la bulle si elle était absente.
Il est important de comprendre que la pression totale en un point du
fluide est la somme de cette grandeur et de la pression
hydorstatique ![]() : cette pression totale peut donc devenir
négative !
: cette pression totale peut donc devenir
négative !
Notations classiques : ![]() ,
, ![]()
Le rayon qu'une bulle constituée de gaz aurait au repos sous des conditions ambiantes données (en général p0 = 1 atm, T0 = 298 K). Ce rayon est bien entendu lié à la quantité de gaz contenue dans la bulle par une équation d'état, la loi des gaz parfaits étant acceptable dans ces conditions standard.
Le rayon ambiant est l'un des paramètres fondamentaux en plus de la pression acoustique et de la fréquence qui détermine le type d'oscillation de la bulle.
Il faut comprendre que ce rayon ambiant peut varier lentement au cours du temps par l'absorption en moyenne d'une petite quantité de gaz dissous sur chaque période acoustique, phénomène appelé diffusion rectifiée.
L'équation de Rayleigh décrit le mouvement d'une bulle de gaz supposée seule dans un liquide incompressible d'extension infinie.
![]() représente le rayon de la bulle,
représente le rayon de la bulle, ![]() la masse volumique du
liquide,
la masse volumique du
liquide, ![]() la pression dans le liquide à la paroi de la bulle,
et
la pression dans le liquide à la paroi de la bulle,
et
![]() la pression infiniment loin de la bulle, ou encore
la pression qui existerait au centre de la bulle si elle était
absente.
la pression infiniment loin de la bulle, ou encore
la pression qui existerait au centre de la bulle si elle était
absente.
La pression ![]() peut être reliée à la pression dans la bulle en
écrivant la continuité des contraintes normales à l'interface:
peut être reliée à la pression dans la bulle en
écrivant la continuité des contraintes normales à l'interface:
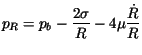 |
Le second terme est lié à la tension superficielle et le troisième à la viscosité du liquide.
La grandeur ![]() est la pression dans la bulle en toute rigueur au niveau de
l'interface. La pression à l'infini peut être représentée, dans le
cas d'un champ acoustique par la somme de la pression hydrostatique
et de la pression engendrée par l'onde acoustique.
est la pression dans la bulle en toute rigueur au niveau de
l'interface. La pression à l'infini peut être représentée, dans le
cas d'un champ acoustique par la somme de la pression hydrostatique
et de la pression engendrée par l'onde acoustique.
L'équation obtenue est celle d'un oscillateur non-linéaire forcé dont les solutions constituent un ensemble très complexe: hystérésis, résonances non-linéaires, bifurcations doublement de période et chaos.
On définit le rayon de résonance
![]() comme le
rayon ambiant d'une bulle dont
la fréquence de résonance serait celle de l'excitation acoustique.
Ainsi, une bulle inférieure à la taille de résonance est excitée à
une fréquence inférieure à sa fréquence de résonance et inversement.
comme le
rayon ambiant d'une bulle dont
la fréquence de résonance serait celle de l'excitation acoustique.
Ainsi, une bulle inférieure à la taille de résonance est excitée à
une fréquence inférieure à sa fréquence de résonance et inversement.
Cette grandeur se détermine implicitement à partir de la définition de la fréquence de résonance. En négligeant l'influence des phénomènes dissipatifs et la tension superficielle, on obtient
![$\displaystyle R_{\text{res}}= \left[\frac{p_0}{\rho\omega^2} 3\eta\right]^{1/2}$](lexique-img28.png) |
où ![]() est l'exposant polytropique. Ce dernier dépendant du rayon
ambiant
est l'exposant polytropique. Ce dernier dépendant du rayon
ambiant ![]() , l'expression ci-dessus serait implicite. On peut
définir (souvent pour simplifier des calculs) le rayon de
résonance isotherme (
, l'expression ci-dessus serait implicite. On peut
définir (souvent pour simplifier des calculs) le rayon de
résonance isotherme (![]() ) dans les calculs.
) dans les calculs.
Pour une excitation à 20 kHz, le rayon de résonance vaut
approximativement 158 ![]() m, alors qu'à 1 MHz il vaut 3.2
m, alors qu'à 1 MHz il vaut 3.2 ![]() m.
m.
Il est important de se rappeler que cette grandeur relève de la théorie linéaire, qui conduit souvent à de mauvaises interprétations des phénomènes. En particulier, la théorie et les expérimentations SBSL pour des fréquences de l'ordre de 20 kHz montrent que des bulles de cette taille ne peuvent exister pour des excitations supérieures à environ 1 atm, en raison des instabilités de surface. Cependant son emploi dans les calculs permet en général une formulation plus simple (25).
Le seuil de Blake est la clé de la cavitation acoustique dite
``transitoire'' ou ``forte'' ou ``instable'' ou plus exactement
``inertielle'', qui engendre des phénomènes chimiques et mécaniques
violents. Il convient avant tout de bien comprendre que ce seuil est
une frontière dans le plan des paramètres ![]() , où
, où ![]() pression acoustique et
pression acoustique et ![]() rayon
ambiant.
rayon
ambiant.
Meme en présence d'une forte dépression, l'expansion d'une bulle de gaz très petite reste limitée à cause de la tension superficielle, qui est inversement proportionnelles au rayon de la bulle. On peut donc obtenir des oscillations quasi-linéaire pour une telle bulle malgré une pression acoustique de l'ordre d'1 atmosphère.
Au-delà du seuil, la tension superficielle ne peut plus contrôler l'expansion, et la bulle subit alors une phase explosive (qui sera suivie par une implosion lors dela phase de recompression de l'onde).
Pour déterminer le seuil, on peut envisager une détente
quasi-statique isotherme d'une bulle de rayon initial ![]() en
diminuant graduellement la pression ambiante dans le liquide
en
diminuant graduellement la pression ambiante dans le liquide ![]() . Le rayon
. Le rayon ![]() de la bulle en équilibre radial serait donnée par:
de la bulle en équilibre radial serait donnée par:
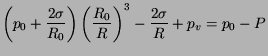 |
Le membre de gauche est la pression dans le liquide au voisinage de
la paroi de la bulle, et celui de droite la pression supposée
uniforme dans tout le liquide. Le membre de gauche possède un
minimum lorsque ![]() varie, par conséquent, lorsque la dépression
varie, par conséquent, lorsque la dépression ![]() est supérieure à une certaine valeur
est supérieure à une certaine valeur ![]() , la relation ci-dessus ne
peut plus être vérifiée et l'équilibre n'est plus possible. Il
apparait un gradient de pression centripète dans le liquide, et le
celui-ci se met en mouvement (centrifuge donc explosif). Il manque
en fait dans l'équation ci-dessus le premier membre de
l'équation de Rayleigh, qui est proportionnelle à l'énergie
cinétique du liquide.
, la relation ci-dessus ne
peut plus être vérifiée et l'équilibre n'est plus possible. Il
apparait un gradient de pression centripète dans le liquide, et le
celui-ci se met en mouvement (centrifuge donc explosif). Il manque
en fait dans l'équation ci-dessus le premier membre de
l'équation de Rayleigh, qui est proportionnelle à l'énergie
cinétique du liquide.
La valeur critique ![]() est appelé seuil de Blake et est obtenu
en cherchant le minimum du membre de gauche de l'expression
ci-dessus. On obtient (sous forme adimensionnelle):
est appelé seuil de Blake et est obtenu
en cherchant le minimum du membre de gauche de l'expression
ci-dessus. On obtient (sous forme adimensionnelle):
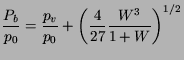 |
où
![]() . Cette équation peut être inversée pour
trouver le rayon critique
. Cette équation peut être inversée pour
trouver le rayon critique ![]() au-delà duquel, à pression acoustique
donnée, une bulle va subir une expansion explosive
(25).
au-delà duquel, à pression acoustique
donnée, une bulle va subir une expansion explosive
(25).
Le raisonnement ci-dessus étant basé sur une évolution
quasi-statique isotherme, il fournit un seuil réaliste pour des
excitations de basse fréquence (![]() doit être très inférieur au
rayon de résonance). A haute fréquence, une séparation
nette entre oscillations faibles et explosives n'existe plus.
doit être très inférieur au
rayon de résonance). A haute fréquence, une séparation
nette entre oscillations faibles et explosives n'existe plus.